Bryson-Denham Problem
Apps.BrysonDenhamProblem History
Show minor edits - Show changes to markup
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/OL4yu4yoHC0" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/OL4yu4yoHC0" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/OL4yu4yoHC0" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)
m = GEKKO()
m = GEKKO(remote=False)
m.Minimize(final*1e5*x**2) m.Minimize(final*1e5*(v+1)**2)
soft = True if soft:
# soft terminal constraint
m.Minimize(final*1e5*x**2)
m.Minimize(final*1e5*(v+1)**2)
else:
# hard terminal constraint
xf = m.Param(); vf = m.Param()
m.free(xf); m.free(vf)
m.fix_final(xf,0); m.fix_final(vf,-1)
# connect endpoint parameters to x and v
m.Equations([xf==x,vf==v])
plt.figure(figsize=(10,6))
- Create a figure
plt.figure(figsize=(10,4))
u = m.Var(value=-6,lb=-6)
u = m.Var(value=-6)
(:html:) <!-- <iframe width="560" height="315" src="https://www.youtube.com/embed/pgJ0jbfFBUE" frameborder="0" allowfullscreen></iframe>
(:htmlend:)
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO() nt = 101; m.time = np.linspace(0,1,nt)
- Variables
x = m.Var(value=0,ub=1/9) v = m.Var(value=1) u = m.Var(value=-6,lb=-6)
p = np.zeros(nt); p[-1] = 1.0 final = m.Param(value=p)
- Equations
m.Equation(x.dt()==v) m.Equation(v.dt()==u)
- Final conditions
m.Minimize(final*1e5*x**2) m.Minimize(final*1e5*(v+1)**2)
- Objective Function
obj = m.Intermediate(0.5*m.integral(u**2)) m.Minimize(final*obj)
m.options.IMODE = 6 m.options.NODES = 2 m.solve()
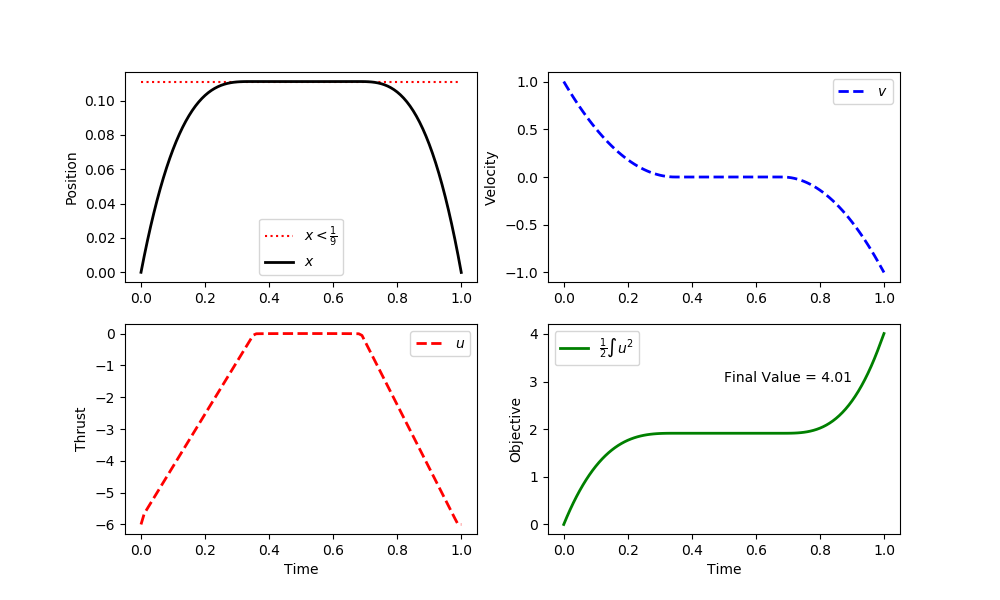
plt.figure(figsize=(10,6)) plt.subplot(2,2,1) plt.plot([0,1],[1/9,1/9],'r:',label=r'$x<\frac{1}{9}$') plt.plot(m.time,x.value,'k-',lw=2,label=r'$x$') plt.ylabel('Position') plt.legend(loc='best') plt.subplot(2,2,2) plt.plot(m.time,v.value,'b--',lw=2,label=r'$v$') plt.ylabel('Velocity') plt.legend(loc='best') plt.subplot(2,2,3) plt.plot(m.time,u.value,'r--',lw=2,label=r'$u$') plt.ylabel('Thrust') plt.legend(loc='best') plt.xlabel('Time') plt.subplot(2,2,4) plt.plot(m.time,obj.value,'g-',lw=2,label=r'$\frac{1}{2} \int u^2$') plt.text(0.5,3.0,'Final Value = '+str(np.round(obj.value[-1],2))) plt.ylabel('Objective') plt.legend(loc='best') plt.xlabel('Time') plt.show() (:sourceend:)


(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)
The parameter u is the acceleration can be adjusted over the time horizon from a starting time of zero to a final time of one. The variable x is the position and v is the velocity.
The parameter u (acceleration) is adjusted over the time horizon from a starting time of zero to a final time of one. The variable x is the position and v is the velocity.
Solution
(:html:) <!-- <iframe width="560" height="315" src="https://www.youtube.com/embed/pgJ0jbfFBUE" frameborder="0" allowfullscreen></iframe>
(:htmlend:)

The parameter u is the acceleration can be adjusted over the time horizon from a starting time of zero to a time of one. The variable x is the position and v is the velocity.
The parameter u is the acceleration can be adjusted over the time horizon from a starting time of zero to a final time of one. The variable x is the position and v is the velocity.
$$\quad \frac{dx(t)}{dt} = v $$
$$\quad \frac{dv(t)}{dt} = u$$
$$\quad x(0) \; = \; x(1) \; = \; 0$$
$$\quad v(0) \; = \; -v(1) \; = \; 1$$
$$\quad x(t) \le \ell, \ell=\frac{1}{9}$$
$$\frac{dx(t)}{dt} = v(t) $$
$$\frac{dv(t)}{dt} = u(t) $$
$$x(0) \; = \; x(1) \; = \; 0$$
$$v(0) \; = \; -v(1) \; = \; 1$$
$$x(t) \le \ell, \; \ell=\frac{1}{9}$$
(:title Bryson-Denham Problem:) (:keywords Benchmark, Python, nonlinear control, dynamic programming, optimal control:) (:description Minimize the integral of the control input while meeting certain path and final time constraints.:)
The Bryson-Denham optimal control problem is a benchmark test problem for optimal control algorithms.
Problem Statement
The parameter u is the acceleration can be adjusted over the time horizon from a starting time of zero to a time of one. The variable x is the position and v is the velocity.
$$\min J = \frac{1}{2} \; \int_0^1 u^2(t) dt$$
$$\mathrm{subject\;to}$$
$$\quad \frac{dx(t)}{dt} = v $$
$$\quad \frac{dv(t)}{dt} = u$$
$$\quad x(0) \; = \; x(1) \; = \; 0$$
$$\quad v(0) \; = \; -v(1) \; = \; 1$$
$$\quad x(t) \le \ell, \ell=\frac{1}{9}$$
(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)