Hock Schittkowski
Apps.HockSchittkowski History
Hide minor edits - Show changes to markup
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the (:html:)<a href="/online/view_pass.php">Online Web-based Interface</a>(:htmlend:)
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the (:html:)<a href="/online/view_pass.php">Online Web-based Interface</a>(:htmlend:) or with Python Gekko.
$$ \mathrm{s.t.} \, x_1 x_2 x_3 x_4 \ge 25$$
$$ \mathrm{subject\;to} \quad x_1 x_2 x_3 x_4 \ge 25$$
$$ s.t. x_1 x_2 x_3 x_4 \ge 25$$
$$ \mathrm{s.t.} \, x_1 x_2 x_3 x_4 \ge 25$$
Example: Hock & Schittkowski Problem #71
Hock & Schittkowski Problem #71
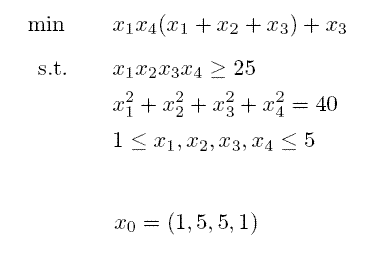
$$ \min x_1 x_4 (x_1 + x_2 + x_3) + x_3 $$
$$ s.t. x_1 x_2 x_3 x_4 \ge 25$$
$$\quad x_1^2 + x_2^2 + x_3^2 + x_4^2 = 40$$
$$\quad 1 \le x_1, x_2, x_3, x_4 \le 5$$
$$\quad x_0 = (1,5,5,1)$$
Corrections and modifications to the Hock-Schittkowski benchmark test set are posted online here along with AMPL and FMCMAP formats. Many thanks to Stephan Seidl (working with Klaus Schittkowski) for making this available.
Corrections and modifications to the Hock-Schittkowski benchmark test set are posted online here along with AMPL and FMCMAP formats. Many thanks to Stephan Seidl for making this available.
Corrections and modifications to the Hock-Schittkowski benchmark test set are posted online here along with AMPL and FMCMAP formats. Many thanks to Stephan Seidl (working with Klaus Schittkowski) for making this available.
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the (:html:)<a href="/online/view_pass.php">Online Web-based Interface</a>(:htmlend:)
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the (:html:)<a href="/online/view_pass.php">Online Web-based Interface</a>(:htmlend:)
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the online submission platform.
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the (:html:)<a href="/online/view_pass.php">Online Web-based Interface</a>(:htmlend:)
Example: Hock & Schittkowski Test Problem #71
Example: Hock & Schittkowski Problem #71
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the online submission platform.
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the online submission platform.
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization.
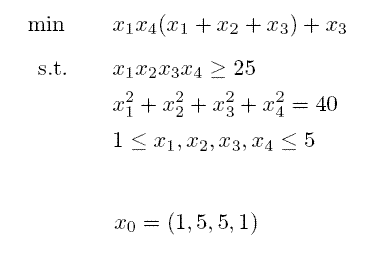
Hock & Schittkowski Test Problem #71
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization. Models may be submitted through the online submission platform.
Individual Files
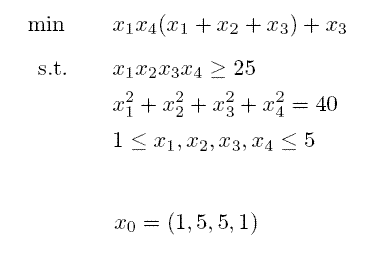
Hock & Schittkowski Test Problem #71
Models presented below are a test suite of optimization problems collected by Hock and Schittkowski. They are part of the test suite used to verify modifications to the APMonitor software. Users may also find this collection useful to compare APMonitor syntax to other modeling languages, for solver benchmarking, or as example problems in optimization.
Hock & Schittkowski Test Problem #71
Complete Collection
Equivalent AMPL models can be found at: https://www.princeton.edu/~rvdb/ampl/nlmodels/hs/index.html
- hs01.apm Δ
- hs02.apm Δ
- hs03.apm Δ
- hs04.apm Δ
- hs05.apm Δ
- hs06.apm Δ
- hs07.apm Δ
- hs08.apm Δ
- hs09.apm Δ
- hs10.apm Δ
- hs11.apm Δ
- hs12.apm Δ
- hs13.apm Δ
- hs14.apm Δ
- hs15.apm Δ
- hs16.apm Δ
- hs17.apm Δ
- hs18.apm Δ
- hs19.apm Δ
- hs20.apm Δ
- hs21.apm Δ
- hs22.apm Δ
- hs23.apm Δ
- hs24.apm Δ
- hs25.apm Δ
- hs26.apm Δ
- hs27.apm Δ
- hs28.apm Δ
- hs29.apm Δ
- hs30.apm Δ
- hs31.apm Δ
- hs32.apm Δ
- hs33.apm Δ
- hs34.apm Δ
- hs35.apm Δ
- hs36.apm Δ
- hs37.apm Δ
- hs38.apm Δ
- hs39.apm Δ
- hs40.apm Δ
- hs41.apm Δ
- hs42.apm Δ
- hs43.apm Δ
- hs44.apm Δ
- hs45.apm Δ
- hs46.apm Δ
- hs47.apm Δ
- hs48.apm Δ
- hs49.apm Δ
- hs50.apm Δ
- hs51.apm Δ
- hs52.apm Δ
- hs53.apm Δ
- hs54.apm Δ
- hs55.apm Δ
- hs56.apm Δ
- hs57.apm Δ
- hs58.apm Δ
- hs59.apm Δ
- hs60.apm Δ
- hs61.apm Δ
- hs62.apm Δ
- hs63.apm Δ
- hs64.apm Δ
- hs65.apm Δ
- hs66.apm Δ
- hs67.apm Δ
- hs68.apm Δ
- hs69.apm Δ
- hs70.apm Δ
- hs71.apm Δ
- hs72.apm Δ
- hs73.apm Δ
- hs74.apm Δ
- hs75.apm Δ
- hs76.apm Δ
- hs77.apm Δ
- hs78.apm Δ
- hs79.apm Δ
- hs80.apm Δ
- hs81.apm Δ
- hs82.apm Δ
- hs83.apm Δ
- hs84.apm Δ
- hs85.apm Δ
- hs86.apm Δ
- hs87.apm Δ
- hs88.apm Δ
- hs89.apm Δ
- hs90.apm Δ
- hs91.apm Δ
- hs92.apm Δ
- hs93.apm Δ
- hs94.apm Δ
- hs95.apm Δ
- hs96.apm Δ
- hs97.apm Δ
- hs98.apm Δ
- hs99.apm Δ
- hs001.apm
- hs002.apm
- hs003.apm
- hs004.apm
- hs005.apm
- hs006.apm
- hs007.apm
- hs008.apm
- hs009.apm
- hs010.apm
- hs011.apm
- hs012.apm
- hs013.apm
- hs014.apm
- hs015.apm
- hs016.apm
- hs017.apm
- hs018.apm
- hs019.apm
- hs020.apm
- hs021.apm
- hs022.apm
- hs023.apm
- hs024.apm
- hs025.apm
- hs026.apm
- hs027.apm
- hs028.apm
- hs029.apm
- hs030.apm
- hs031.apm
- hs032.apm
- hs033.apm
- hs034.apm
- hs035.apm
- hs036.apm
- hs037.apm
- hs038.apm
- hs039.apm
- hs040.apm
- hs041.apm
- hs042.apm
- hs043.apm
- hs044.apm
- hs045.apm
- hs046.apm
- hs047.apm
- hs048.apm
- hs049.apm
- hs050.apm
- hs051.apm
- hs052.apm
- hs053.apm
- hs054.apm
- hs055.apm
- hs056.apm
- hs057.apm
- hs058.apm
- hs059.apm
- hs060.apm
- hs061.apm
- hs062.apm
- hs063.apm
- hs064.apm
- hs065.apm
- hs066.apm
- hs067.apm
- hs068.apm
- hs069.apm
- hs070.apm
- hs071.apm
- hs072.apm
- hs073.apm
- hs074.apm
- hs075.apm
- hs076.apm
- hs077.apm
- hs078.apm
- hs079.apm
- hs080.apm
- hs081.apm
- hs082.apm
- hs083.apm
- hs084.apm
- hs085.apm
- hs086.apm
- hs087.apm
- hs088.apm
- hs089.apm
- hs090.apm
- hs091.apm
- hs092.apm
- hs093.apm
- hs094.apm
- hs095.apm
- hs096.apm
- hs097.apm
- hs098.apm
- hs099.apm
Hock & Schittkowski Models
- hs01.apm Δ
- hs02.apm Δ
- hs03.apm Δ
- hs04.apm Δ
- hs05.apm Δ
- hs06.apm Δ
- hs07.apm Δ
- hs08.apm Δ
- hs09.apm Δ
- hs10.apm Δ
- hs11.apm Δ
- hs12.apm Δ
- hs13.apm Δ
- hs14.apm Δ
- hs15.apm Δ
- hs16.apm Δ
- hs17.apm Δ
- hs18.apm Δ
- hs19.apm Δ
- hs20.apm Δ
- hs21.apm Δ
- hs22.apm Δ
- hs23.apm Δ
- hs24.apm Δ
- hs25.apm Δ
- hs26.apm Δ
- hs27.apm Δ
- hs28.apm Δ
- hs29.apm Δ
- hs30.apm Δ
- hs31.apm Δ
- hs32.apm Δ
- hs33.apm Δ
- hs34.apm Δ
- hs35.apm Δ
- hs36.apm Δ
- hs37.apm Δ
- hs38.apm Δ
- hs39.apm Δ
- hs40.apm Δ
- hs41.apm Δ
- hs42.apm Δ
- hs43.apm Δ
- hs44.apm Δ
- hs45.apm Δ
- hs46.apm Δ
- hs47.apm Δ
- hs48.apm Δ
- hs49.apm Δ
- hs50.apm Δ
- hs51.apm Δ
- hs52.apm Δ
- hs53.apm Δ
- hs54.apm Δ
- hs55.apm Δ
- hs56.apm Δ
- hs57.apm Δ
- hs58.apm Δ
- hs59.apm Δ
- hs60.apm Δ
- hs61.apm Δ
- hs62.apm Δ
- hs63.apm Δ
- hs64.apm Δ
- hs65.apm Δ
- hs66.apm Δ
- hs67.apm Δ
- hs68.apm Δ
- hs69.apm Δ
- hs70.apm Δ
- hs71.apm Δ
- hs72.apm Δ
- hs73.apm Δ
- hs74.apm Δ
- hs75.apm Δ
- hs76.apm Δ
- hs77.apm Δ
- hs78.apm Δ
- hs79.apm Δ
- hs80.apm Δ
- hs81.apm Δ
- hs82.apm Δ
- hs83.apm Δ
- hs84.apm Δ
- hs85.apm Δ
- hs86.apm Δ
- hs87.apm Δ
- hs88.apm Δ
- hs89.apm Δ
- hs90.apm Δ
- hs91.apm Δ
- hs92.apm Δ
- hs93.apm Δ
- hs94.apm Δ
- hs95.apm Δ
- hs96.apm Δ
- hs97.apm Δ
- hs98.apm Δ
- hs99.apm Δ
- hs100.apm
- hs101.apm
- hs102.apm
- hs103.apm
- hs104.apm
- hs105.apm
- hs106.apm
- hs107.apm
- hs108.apm
- hs109.apm
- hs110.apm
- hs111.apm
- hs112.apm
- hs113.apm
- hs114.apm
- hs115.apm
- hs116.apm
- hs117.apm
- hs118.apm
- hs119.apm
Equivalent AMPL models can be found at: https://www.princeton.edu/~rvdb/ampl/nlmodels/hs/index.html