State Space Model Object
Apps.LinearStateSpace History
Hide minor edits - Show changes to markup
u[1].lower = -5 u[1].upper = 5 u[1].dcost = 1 u[1].status = 1
u[0].lower = -5 u[0].upper = 5 u[0].dcost = 1 u[0].status = 1
plt.legend()
plt.legend()
GEKKO Usage: x,y,u = m.state_space(A,B,C) Optional arguments: D=None,E=None, discrete=False,dense=False
GEKKO Usage: x,y,u = m.state_space(A,B,C,D=None) Other optional arguments: E=None,discrete=False,dense=False
GEKKO Usage: x,y,u = m.state_space(A,B,C,D=None,E=None, discrete=False,dense=False)
GEKKO Usage: x,y,u = m.state_space(A,B,C) Optional arguments: D=None,E=None, discrete=False,dense=False
Data: A, B, C, and D matrices
Data: A, B, C, D, and E matrices
GEKKO Usage: x,y,u = m.state_space(A,B,C,D=None)
GEKKO Usage: x,y,u = m.state_space(A,B,C,D=None,E=None, discrete=False,dense=False)
$$\dot x = A x + B u$$
$$E\dot x = A x + B u$$
$$E \in \mathbb{R}^{n \, \mathrm{x} \, n}$$
Also see Discrete State Space and State Space Introduction
Also see:
- State Space Introduction
- Discrete State Space
- ARX Time Series
(:title State Space Models:)
(:title State Space Model Object:)
(:title APMonitor and GEKKO State Space Models:)
(:title State Space Models:)
Also see Discrete State Space
Also see Discrete State Space and State Space Introduction
Linear Model Predictive Control
(:title APMonitor and GEKKO State Space Models:) (:keywords linear, state space, stability, dynamic, multiple input, multiple output, MIMO, model predictive control:) (:description Linear Time Invariant (LTI) state space models are a linear representation of a dynamic system in either discrete or continuous time. Examples show how to use continuous LTI state space models in APMonitor and GEKKO.:)
Type: Object Data: A, B, C, and D matrices Inputs: Input (u) Outputs: States (x), Output (y) Description: LTI State Space Model APMonitor Usage: sys = lti GEKKO Usage: x,y,u = m.state_space(A,B,C,D=None)
Linear Time Invariant (LTI) state space models are a linear representation of a dynamic system in either discrete or continuous time. Putting a model into state space form is the basis for many methods in process dynamics and control analysis. Below is the continuous time form of a model in state space form.
$$\dot x = A x + B u$$
$$y = C x + D u$$
with states `x in \mathbb{R}^n` and state derivatives `\dot x = {dx}/{dt} in \mathbb{R}^n`. The notation `in \mathbb{R}^n` means that `x` and `\dot x` are in the set of real-numbered vectors of length `n`. The other elements are the outputs `y in \mathbb{R}^p`, the inputs `u in \mathbb{R}^m`, the state transition matrix `A`, the input matrix `B`, and the output matrix `C`. The remaining matrix `D` is typically zeros because the inputs do not typically affect the outputs directly. The dimensions of each matrix are shown below with `m` inputs, `n` states, and `p` outputs.
$$A \in \mathbb{R}^{n \, \mathrm{x} \, n}$$ $$B \in \mathbb{R}^{n \, \mathrm{x} \, m}$$ $$C \in \mathbb{R}^{p \, \mathrm{x} \, n}$$ $$D \in \mathbb{R}^{p \, \mathrm{x} \, m}$$
Example Model Predictive Control in GEKKO
Example Model Predictive Control in GEKKO
Example Model
Example Model in APMonitor
Example Model Predictive Control in GEKKO
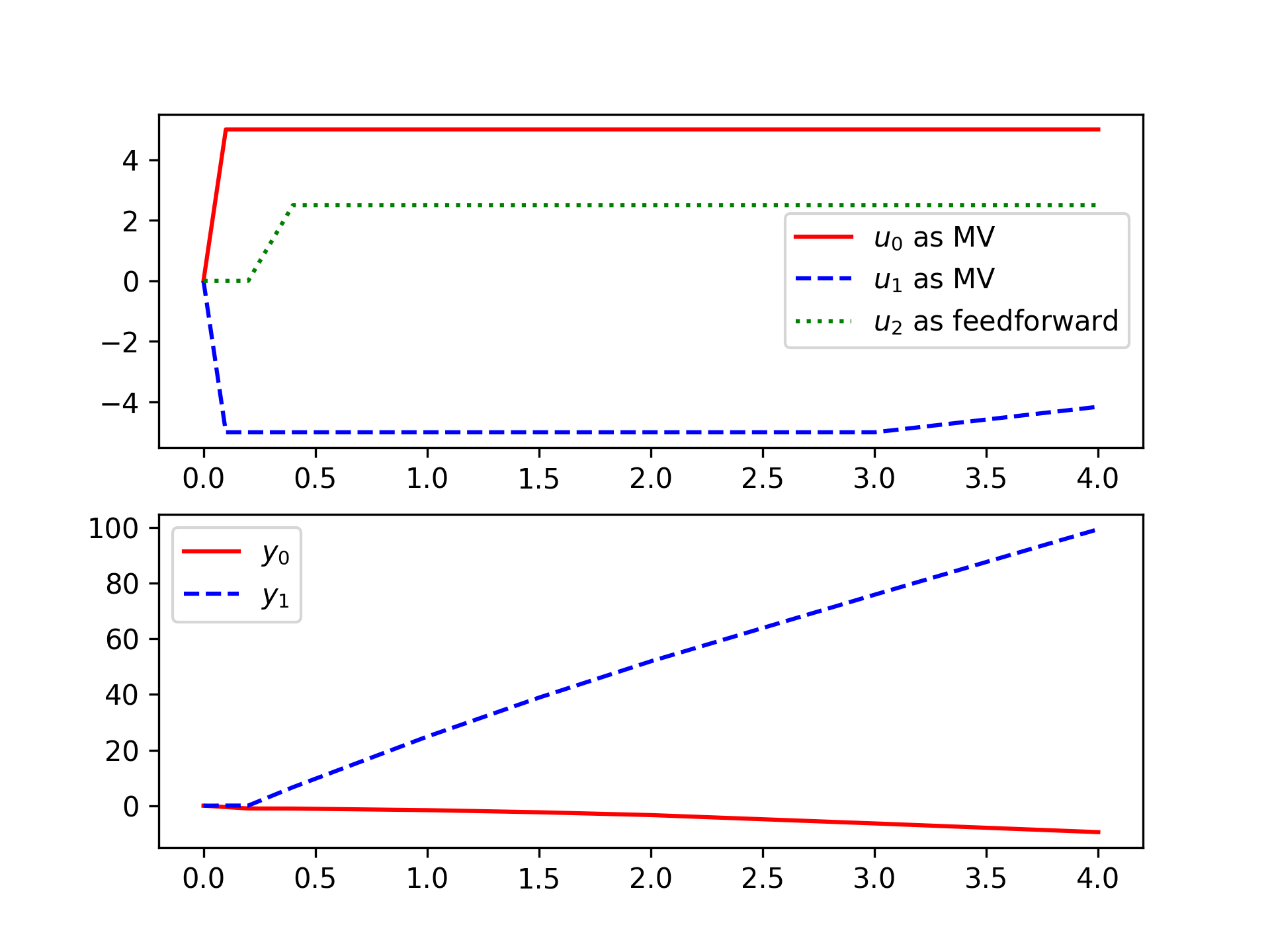
(:source lang=python:) import numpy as np from gekko import GEKKO
A = np.array([[-.003, 0.039, 0, -0.322],
[-0.065, -0.319, 7.74, 0],
[0.020, -0.101, -0.429, 0],
[0, 0, 1, 0]])
B = np.array([[0.01, 1, 2],
[-0.18, -0.04, 2],
[-1.16, 0.598, 2],
[0, 0, 2]]
)
C = np.array([[1, 0, 0, 0],
[0, -1, 0, 7.74]])
- Build GEKKO State Space model
m = GEKKO() x,y,u = m.state_space(A,B,C,D=None)
- customize names
- MVs
mv0 = u[0] mv1 = u[1]
- Feedforward
ff0 = u[2]
- CVs
cv0 = y[0] cv1 = y[1]
m.time = [0, 0.1, 0.2, 0.4, 1, 1.5, 2, 3, 4] m.options.imode = 6 m.options.nodes = 3
u[1].lower = -5 u[1].upper = 5 u[1].dcost = 1 u[1].status = 1
u[1].lower = -5 u[1].upper = 5 u[1].dcost = 1 u[1].status = 1
- CV tuning
- tau = first order time constant for trajectories
y[0].tau = 5 y[1].tau = 8
- tr_init = 0 (dead-band)
- = 1 (first order trajectory)
- = 2 (first order traj, re-center with each cycle)
y[0].tr_init = 0 y[1].tr_init = 0
- targets (dead-band needs upper and lower values)
- SPHI = upper set point
- SPLO = lower set point
y[0].sphi= -8.5 y[0].splo= -9.5 y[1].sphi= 5.4 y[1].splo= 4.6
y[0].status = 1 y[1].status = 1
- feedforward
u[2].status = 0 u[2].value = np.zeros(np.size(m.time)) u[2].value[3:] = 2.5
m.solve() # (GUI=True)
- also create a Python plot
import matplotlib.pyplot as plt
plt.subplot(2,1,1) plt.plot(m.time,mv0.value,'r-',label=r'$u_0$ as MV') plt.plot(m.time,mv1.value,'b--',label=r'$u_1$ as MV') plt.plot(m.time,ff0.value,'g:',label=r'$u_2$ as feedforward') plt.subplot(2,1,2) plt.plot(m.time,cv0.value,'r-',label=r'$y_0$') plt.plot(m.time,cv1.value,'b--',label=r'$y_1$') plt.show() (:sourceend:)
File *.mpc.txt
File mpc.txt
File *.mpc.a.txt
File mpc.a.txt
File *.mpc.b.txt
File mpc.b.txt
File *.mpc.c.txt
File mpc.c.txt
File *.mpc.d.txt
File mpc.d.txt
Model control
Objects
mpc = lti
End Objects
End Model
Model control
Objects
mpc = lti
End Objects
End Model
File *.mpc.txt
sparse, continuous ! dense/sparse, continuous/discrete 2 ! m=number of inputs 3 ! n=number of states 3 ! p=number of outputs
End File
File *.mpc.txt sparse, continuous ! dense/sparse, continuous/discrete 2 ! m=number of inputs 3 ! n=number of states 3 ! p=number of outputs End File
File *.mpc.a.txt
1 1 0.9 2 2 0.1 3 3 0.5
End File
File *.mpc.a.txt 1 1 0.9 2 2 0.1 3 3 0.5 End File
File *.mpc.b.txt
1 1 1.0 2 2 1.0 3 1 0.5 3 2 0.5
End File
File *.mpc.b.txt 1 1 1.0 2 2 1.0 3 1 0.5 3 2 0.5 End File
File *.mpc.c.txt
1 1 0.5 2 2 1.0 3 3 2.0
End File
File *.mpc.c.txt 1 1 0.5 2 2 1.0 3 3 2.0 End File
File *.mpc.d.txt
1 1 0.2
End File
File *.mpc.d.txt 1 1 0.2 End File
Example Model
new linear time-invariant object
Example Model
! new linear time-invariant object
Model information
continuous form
dx/dt = A * x + B * u
y = C * x + D * u
dimensions
(nx1) = (nxn)*(nx1) + (nxm)*(mx1)
(px1) = (pxn)*(nx1) + (pxm)*(mx1)
discrete form
x[k+1] = A * x[k] + B * u[k]
y[k] = C * x[k] + D * u[k]
! Model information ! continuous form ! dx/dt = A * x + B * u ! y = C * x + D * u ! ! dimensions ! (nx1) = (nxn)*(nx1) + (nxm)*(mx1) ! (px1) = (pxn)*(nx1) + (pxm)*(mx1) ! ! discrete form ! x[k+1] = A * x[k] + B * u[k] ! y[k] = C * x[k] + D * u[k]
A matrix (row, column, value)
! A matrix (row, column, value)
B matrix (row, column, value)
! B matrix (row, column, value)
C matrix (row, column, value)
! C matrix (row, column, value)
D matrix (row, column, value)
! D matrix (row, column, value)

Example Model
new linear time-invariant object
Model control
Objects
mpc = lti
End Objects
End Model
Model information
continuous form
dx/dt = A * x + B * u
y = C * x + D * u
dimensions
(nx1) = (nxn)*(nx1) + (nxm)*(mx1)
(px1) = (pxn)*(nx1) + (pxm)*(mx1)
discrete form
x[k+1] = A * x[k] + B * u[k]
y[k] = C * x[k] + D * u[k]
File *.mpc.txt
sparse, continuous ! dense/sparse, continuous/discrete 2 ! m=number of inputs 3 ! n=number of states 3 ! p=number of outputs
End File
A matrix (row, column, value)
File *.mpc.a.txt
1 1 0.9 2 2 0.1 3 3 0.5
End File
B matrix (row, column, value)
File *.mpc.b.txt
1 1 1.0 2 2 1.0 3 1 0.5 3 2 0.5
End File
C matrix (row, column, value)
File *.mpc.c.txt
1 1 0.5 2 2 1.0 3 3 2.0
End File
D matrix (row, column, value)
File *.mpc.d.txt
1 1 0.2
End File
These models are typically in the finite impulse response form or linear state space form. Either model form can be converted to an APMonitor for a linear MPC upgrade. Once the linear MPC model is converted, nonlinear elements can be added to avoid multiple model switching, gain scheduling, or other ad hoc measures commonly employed because of linear MPC restrictions.
These models are typically in the finite impulse response form or linear state space form. Either model form can be converted to an APMonitor for a linear MPC upgrade. Once in APMonitor form, nonlinear elements can be added to avoid multiple model switching, gain scheduling, or other ad hoc measures commonly employed because of linear MPC restrictions.
These models are typically in the finite impulse response form or linear state space form. Either model form can be converted to an APMonitor for a linear MPC upgrade. Once the linear MPC model is converted, nonlinear elements can be added to avoid multiple model switching, gain scheduling, or other ad hoc measures commonly employed because of linear MPC shortcomings.
These models are typically in the finite impulse response form or linear state space form. Either model form can be converted to an APMonitor for a linear MPC upgrade. Once the linear MPC model is converted, nonlinear elements can be added to avoid multiple model switching, gain scheduling, or other ad hoc measures commonly employed because of linear MPC restrictions.
Linear model predictive controllers are based on models in the finite impulse response form or linear state space form. Either model form can be converted to a form that APMonitor uses for estimation and control.
Model Predictive Control, or MPC, is an advanced method of process control that has been in use in the process industries such as chemical plants and oil refineries since the 1980s. Model predictive controllers rely on dynamic models of the process, most often linear empirical models obtained by system identification.
These models are typically in the finite impulse response form or linear state space form. Either model form can be converted to an APMonitor for a linear MPC upgrade. Once the linear MPC model is converted, nonlinear elements can be added to avoid multiple model switching, gain scheduling, or other ad hoc measures commonly employed because of linear MPC shortcomings.
Linear State Space Model
Linear Model Predictive Control
Linear model predictive controllers are based on models in the finite impulse response form or linear state space form. Either model form can be converted to a form that APMonitor uses for estimation and control.
