Nonlinear and Multivariate Regression
Objective: Perform nonlinear and multivariate regression on energy data to predict oil price.
Predictors are data features that are inputs to calculate a predicted output. In machine learning the data inputs are called features and the measured outputs are called labels. Regression is the method of adjusting parameters in a model to minimize the difference between the predicted output and the measured output. The objective of this problem is to predict the price of oil (OIL) from indicator features that include West Texas Intermediate (WTI) price, Henry Hub gas price (HH), and the Mont Belvieu (MB) propane spot price. Data is available for OIL, WTI, HH, and MB from the years 2000 to 2016 at the following link.
Use the following nonlinear correlation with unknown parameters A, B, C, and D.
$$OIL = A \, \left(WTI^B\right) \, \left(HH^C\right) \, \left(MB^D\right)$$
This particular nonlinear equation can be transformed to a linear equation with a log transformation as
$$\log(OIL)=\log(A)+B\log(WTI)+C\log(HH)+D\log(MB)$$
or kept in the original nonlinear form. Adjust the unknown parameters (A, B, C, D) to minimize a sum of squared errors of the normalized difference between the measured and predicted value. Normalize the difference by the measured value before the it is squared.
$$\min_{A,B,C,D} \sum_{i=1}^n \left( \frac{OIL_{pred,i}-OIL_{meas,i}}{OIL_{meas,i}} \right)^2$$
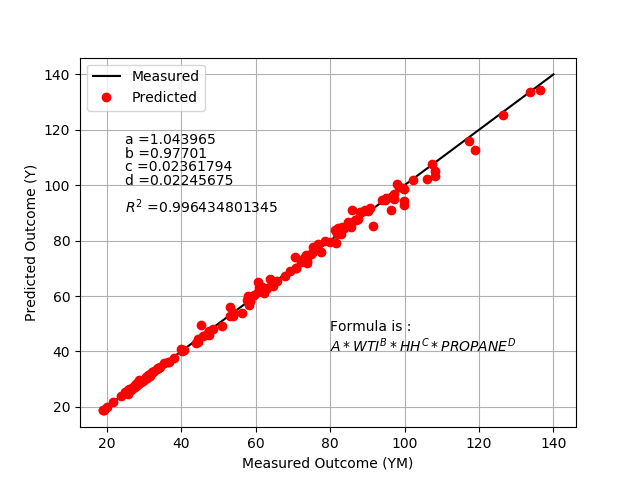
where n is the number of data points, i is an index for the current measured value, pred is the predicted value, and meas is the measured value. Report the parameter values, the R2 value of fit, and display a plot of the results.
Python (GEKKO) Solution
# solve for oil sales price (outcome)
# using 3 predictors of WTI Oil Price,
# Henry Hub Price and MB Propane Spot Price
import numpy as np
# use 'pip install gekko' to get package
from gekko import GEKKO
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# data file from URL address
data = 'https://apmonitor.com/me575/uploads/Main/oil_data.txt'
df = pd.read_csv(data)
xm1 = np.array(df["WTI_PRICE"]) # WTI Oil Price
xm2 = np.array(df["HH_PRICE"]) # Henry Hub Gas Price
xm3 = np.array(df["NGL_PRICE"]) # MB Propane Spot Price
ym = np.array(df["BEST_PRICE"]) # oil sales price
# GEKKO model
m = GEKKO()
a = m.FV(lb=-100.0,ub=100.0)
b = m.FV(lb=-100.0,ub=100.0)
c = m.FV(lb=-100.0,ub=100.0)
d = m.FV(lb=-100.0,ub=100.0)
x1 = m.Param(value=xm1)
x2 = m.Param(value=xm2)
x3 = m.Param(value=xm3)
z = m.Param(value=ym)
y = m.Var()
m.Equation(y==a*(x1**b)*(x2**c)*(x3**d))
m.Minimize(((y-z)/z)**2)
# Options
a.STATUS = 1
b.STATUS = 1
c.STATUS = 1
d.STATUS = 1
m.options.IMODE = 2
m.options.SOLVER = 1
# Solve
m.solve()
print('a: ', a.value[0])
print('b: ', b.value[0])
print('c: ', c.value[0])
print('d: ', d.value[0])
cFormula = "Formula is : " + "\n" + \
r"$A * WTI^B * HH^C * PROPANE^D$"
from scipy import stats
slope, intercept, r_value, p_value, \
std_err = stats.linregress(ym,y)
r2 = r_value**2
cR2 = "R^2 correlation = " + str(r_value**2)
print(cR2)
# plot solution
plt.figure(1)
plt.plot([20,140],[20,140],'k-',label='Measured')
plt.plot(ym,y,'ro',label='Predicted')
plt.xlabel('Measured Outcome (YM)')
plt.ylabel('Predicted Outcome (Y)')
plt.legend(loc='best')
plt.text(25,115,'a =' + str(a.value[0]))
plt.text(25,110,'b =' + str(b.value[0]))
plt.text(25,105,'c =' + str(c.value[0]))
plt.text(25,100,'d =' + str(d.value[0]))
plt.text(25,90,r'$R^2$ =' + str(r_value**2))
plt.text(80,40,cFormula)
plt.grid(True)
plt.show()
Python (SciPy) Solution
# solve for oil sales price (outcome)
# using 3 predictors of WTI Oil Price,
# Henry Hub Price and MB Propane Spot Price
import numpy as np
from scipy.optimize import minimize
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# data file from URL address
data = 'https://apmonitor.com/me575/uploads/Main/oil_data.txt'
df = pd.read_csv(data)
xm1 = np.array(df["WTI_PRICE"]) # WTI Oil Price
xm2 = np.array(df["HH_PRICE"]) # Henry Hub Gas Price
xm3 = np.array(df["NGL_PRICE"]) # MB Propane Spot Price
ym = np.array(df["BEST_PRICE"]) # oil sales price received (outcome)
# calculate y
def calc_y(x):
a = x[0]
b = x[1]
c = x[2]
d = x[3]
#y = a * xm1 + b # linear regression
y = a * ( xm1 ** b ) * ( xm2 ** c ) * ( xm3 ** d )
return y
# define objective
def objective(x):
# calculate y
y = calc_y(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + ((y[i]-ym[i])/ym[i])**2
# return result
return obj
# initial guesses
x0 = np.zeros(4)
x0[0] = 0.0 # a
x0[1] = 0.0 # b
x0[2] = 0.0 # c
x0[3] = 0.0 # d
# show initial objective
print('Initial Objective: ' + str(objective(x0)))
# optimize
# bounds on variables
my_bnds = (-100.0, 100.0)
bnds = (my_bnds, my_bnds, my_bnds, my_bnds)
solution = minimize(objective, x0, method='SLSQP', bounds=bnds)
x = solution.x
y = calc_y(x)
# show final objective
cObjective = 'Final Objective: ' + str(objective(x))
print(cObjective)
# print solution
print('Solution')
cA = 'A = ' + str(x[0])
print(cA)
cB = 'B = ' + str(x[1])
print(cB)
cC = 'C = ' + str(x[2])
print(cC)
cD = 'D = ' + str(x[3])
print(cD)
cFormula = "Formula is : " + "\n" \
+ "A * WTI^B * HH^C * PROPANE^D"
cLegend = cFormula + "\n" + cA + "\n" + cB + "\n" \
+ cC + "\n" + cD + "\n" + cObjective
#ym measured outcome
#y predicted outcome
from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(ym,y)
r2 = r_value**2
cR2 = "R^2 correlation = " + str(r_value**2)
print(cR2)
# plot solution
plt.figure(1)
plt.title('Actual (YM) versus Predicted (Y) Outcomes For Non-Linear Regression')
plt.plot(ym,y,'o')
plt.xlabel('Measured Outcome (YM)')
plt.ylabel('Predicted Outcome (Y)')
plt.legend([cLegend])
plt.grid(True)
plt.show()
Thanks to Fulton Loebel for submitting this example problem to the APMonitor Discussion Forum.
There is additional information about regression in the Data Science Online Course.

