Piecewise Linear
Apps.PiecewiseLinear History
Show minor edits - Show changes to markup
(:html:)<font size=2><pre>
(:source lang=python:)
</pre></font> (:htmlend:)
(:sourceend:)
(:html:)<font size=2><pre>
(:source lang=python:)
</pre></font> (:htmlend:)
(:sourceend:)
(:html:)<font size=2><pre>
(:source lang=python:)
</pre></font> (:htmlend:)
(:sourceend:)

from scipy import optimize
PWL in GEKKO Python

(:source lang=python:) from scipy import optimize import matplotlib.pyplot as plt from gekko import GEKKO import numpy as np
m = GEKKO() m.options.SOLVER = 1
xz = m.FV(value = 4.5) yz = m.Var()
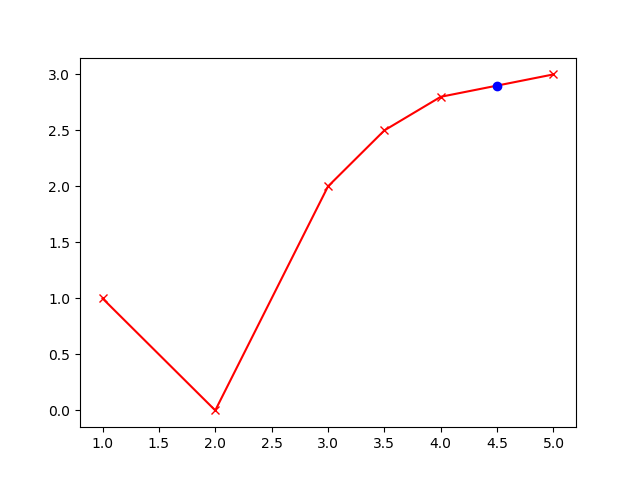
xp_val = np.array([1, 2, 3, 3.5, 4, 5]) yp_val = np.array([1, 0, 2, 2.5, 2.8, 3]) xp = [m.Param(value=xp_val[i]) for i in range(6)] yp = [m.Param(value=yp_val[i]) for i in range(6)]
x = [m.Var(lb=xp[i],ub=xp[i+1]) for i in range(5)] x[0].lower = -1e20 x[-1].upper = 1e20
- Variables
slk_u = [m.Var(value=1,lb=0) for i in range(4)] slk_l = [m.Var(value=1,lb=0) for i in range(4)]
- Intermediates
slope = [] for i in range(5):
slope.append(m.Intermediate((yp[i+1]-yp[i]) / (xp[i+1]-xp[i])))
y = [] for i in range(5):
y.append(m.Intermediate((x[i]-xp[i])*slope[i]))
for i in range(4):
m.Obj(slk_u[i] + slk_l[i])
m.Equation(xz == x[0] + slk_u[0]) for i in range(3):
m.Equation(xz == x[i+1] + slk_u[i+1] - slk_l[i])
m.Equation(xz == x[4] - slk_l[3])
m.Equation(yz == yp[0] + y[0] + y[1] + y[2] + y[3] + y[4])
m.solve()
plt.plot(xp,yp,'rx-',label='PWL function') plt.plot(xz,yz,'bo',label='Data') plt.show() (:sourceend:)
APMonitor PWL Object
Model pwl
File p.txt
1, 1
2, 0
3, 2
3.5, 2.5
4, 2.8
5, 3
End File
Objects
p = pwl
End Objects
Connections
x = p.x
y = p.y
End Connections
! data points
xp[1] = 1
yp[1] = 1
xp[2] = 2
yp[2] = 0
xp[3] = 3
yp[3] = 2
xp[4] = 3.5
yp[4] = 2.5
xp[5] = 4
yp[5] = 2.8
xp[6] = 5
yp[6] = 3
! piece-wise linear segments
x[1] <=xp[2]
x[2:4] >xp[2:4], <=xp[3:5]
x[5] >xp[5]
! slack variables
slk_u[1:4]
slk_l[2:5]
</pre></font> (:htmlend:)
Equivalent Problem with Slack Variables
(:html:)<font size=2><pre>
Parameters
! independent variable
x = 6.0
! data points
xp[1] = 1
yp[1] = 1
xp[2] = 2
yp[2] = 0
xp[3] = 3
yp[3] = 2
xp[4] = 3.5
yp[4] = 2.5
xp[5] = 4
yp[5] = 2.8
xp[6] = 5
yp[6] = 3
End Parameters
Variables
! piece-wise linear segments
x[1] <=xp[2]
x[2:4] >xp[2:4], <=xp[3:5]
x[5] >xp[5]
! dependent variable
y
! slack variables
slk_u[1:4]
slk_l[2:5]
End Variables
End Model
In Situ Adaptive Tabulation (ISAT) is an example of a multi-dimensional piecewise linear approximation. The piecewise linear segments are built dynamically as new data becomes available. This way, only regions that are accessed in practice contribute to the function approximation.
In Situ Adaptive Tabulation (ISAT) is an example of a multi-dimensional piecewise linear approximation. The piecewise linear segments are built dynamically as new data becomes available. This way, only regions that are accessed in practice contribute to the function approximation.
minimize slk_u[1:4]
minimize slk_l[2:5]
File *.m.csv
File m.csv
End Equations
End Model </pre></font> (:htmlend:)
(:html:)<font size=2><pre>
Piece-wise function with the LOOKUP object
create the csv file
File *.m.csv
input, y[1], y[2]
1, 2, 4
3, 4, 6
5, -5, -7
-1, 1, 0.5
End File
define lookup object m
Objects
m = lookup
End Objects
connect m properties with model parameters
Connections
x = m.input y[1] = m.y[1] y[2] = m.y[2]
End Connections
simple model
Model n
Parameters
x = 1
y[1]
y[2]
End Parameters
Variables
y
End Variables
Equations
y = y[1]+y[2]
(:html:)<font size=1><pre>
(:html:)<font size=2><pre>
(:htmlend:)
(:htmlend:)
(:html:)<font size=1><pre> Model pwl
Parameters
! independent variable
x = 6.0
! data points
xp[1] = 1
yp[1] = 1
xp[2] = 2
yp[2] = 0
xp[3] = 3
yp[3] = 2
xp[4] = 3.5
yp[4] = 2.5
xp[5] = 4
yp[5] = 2.8
xp[6] = 5
yp[6] = 3
End Parameters
Variables
! piece-wise linear segments
x[1] <=xp[2]
x[2:4] >xp[2:4], <=xp[3:5]
x[5] >xp[5]
! dependent variable
y
! slack variables
slk_u[1:4]
slk_l[2:5]
End Variables
Intermediates
slope[1:5] = (yp[2:6]-yp[1:5]) / (xp[2:6]-xp[1:5])
y[1:5] = (x[1:5]-xp[1:5])*slope[1:5]
End Intermediates
Equations
x = x[1] + slk_u[1]
x = x[2:4] + slk_u[2:4] - slk_l[2:4]
x = x[5] - slk_l[5]
y = yp[1] + y[1] + y[2] + y[3] + y[4] + y[5]
End Equations
End Model </pre></font> (:htmlend:)
Piece-wise Linear Approximation
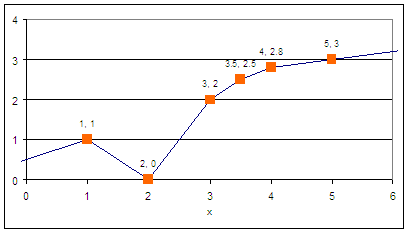
A piece-wise linear function is an approximation of a nonlinear relationship. For more nonlinear relationships, additional linear segments are added to refine the approximation.
As an example, the piecewise linear form is often used to approximate valve characterization (valve position (% open) to flow). This is a single input-single output function approximation.
In Situ Adaptive Tabulation (ISAT) is an example of a multi-dimensional piecewise linear approximation. The piecewise linear segments are built dynamically as new data becomes available. This way, only regions that are accessed in practice contribute to the function approximation.