GEKKO Python Tutorials
GEKKO Python is designed for large-scale optimization and accesses solvers of constrained, unconstrained, continuous, and discrete problems. Problems in linear programming, quadratic programming, integer programming, nonlinear optimization, systems of dynamic nonlinear equations, and multi-objective optimization can be solved. The platform can find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into external modeling and analysis software. It is free for academic and commercial use under the MIT license.

The GEKKO package is available through the package manager pip in Python.
pip install gekko
Another method to obtain GEKKO is to include the following code snippet at the beginning of a Python script. If GEKKO is not available, it uses the pip module to install it.
from pip import main as pipmain
except:
from pip._internal import main as pipmain
pipmain(['install','gekko'])
# to upgrade: pipmain(['install','--upgrade','gekko'])
Gekko source code is available on GitHub. It is downloaded over 100,000 times per month according to PyPi stats.
Star
GEKKO Information
The latest GEKKO source is available on GitHub. Download statistics are available from the PyPI Stats Website. Functionality is tested with Python 2.7 and Python 3+ for all operating systems (Windows, MacOS, Linux) and architectures (such as ARM processors) that support Python.
If you use GEKKO and publish the results, please consider citing the following article:
- Beal, L.D.R., Hill, D., Martin, R.A., and Hedengren, J. D., GEKKO Optimization Suite, Processes, Volume 6, Number 8, 2018, doi: 10.3390/pr6080106. Article - BibTeX - RIS
There are 18 example problems with GEKKO that are provided below. These examples demonstrate the equation solving, regression, differential equation simulation, nonlinear programming, machine learning, model predictive control, moving horizon estimation, debugging, and other applications. While these applications are designed to be tutorial in nature and very simple, GEKKO references are further application examples of complex and multi-disciplinary systems.
18 Example Applications
m = GEKKO() # create GEKKO model
y = m.Var(value=2) # define new variable, initial value=2
m.Equation(y**2==1) # define new equation
m.options.SOLVER=1 # change solver (1=APOPT,3=IPOPT)
m.solve(disp=False)
print('y: ' + str(y.value)) # print variable value
m = GEKKO() # create GEKKO model
x = m.Var() # define new variable, default=0
y = m.Var() # define new variable, default=0
m.Equations([3*x+2*y==1, x+2*y==0]) # equations
m.solve(disp=False) # solve
print(x.value,y.value) # print solution
m = GEKKO() # create GEKKO model
x = m.Var(value=0) # define new variable, initial value=0
y = m.Var(value=1) # define new variable, initial value=1
m.Equations([x + 2*y==0, x**2+y**2==1]) # equations
m.solve(disp=False) # solve
print([x.value[0],y.value[0]]) # print solution
import numpy as np
import matplotlib.pyplot as plt
xm = np.array([0,1,2,3,4,5])
ym = np.array([0.1,0.2,0.3,0.5,1.0,0.9])
m = GEKKO()
m.x = m.Param(value=np.linspace(-1,6))
m.y = m.Var()
m.options.IMODE=2
m.cspline(m.x,m.y,xm,ym)
m.solve(disp=False)
#help(m.cspline)
p = GEKKO()
p.x = p.Var(value=1,lb=0,ub=5)
p.y = p.Var()
p.cspline(p.x,p.y,xm,ym)
p.Obj(-p.y)
p.solve(disp=False)
plt.plot(xm,ym,'bo',label='data')
plt.plot(m.x.value,m.y.value,'r--',label='cubic spline')
plt.plot(p.x.value,p.y.value,'ko',label='maximum')
plt.legend(loc='best')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
xm = np.array([0,1,2,3,4,5])
ym = np.array([0.1,0.2,0.3,0.5,0.8,2.0])
#### Solution
m = GEKKO()
m.options.IMODE=2
# coefficients
c = [m.FV(value=0) for i in range(4)]
x = m.Param(value=xm)
y = m.CV(value=ym)
y.FSTATUS = 1
# polynomial model
m.Equation(y==c[0]+c[1]*x+c[2]*x**2+c[3]*x**3)
# linear regression
c[0].STATUS=1
c[1].STATUS=1
m.solve(disp=False)
p1 = [c[1].value[0],c[0].value[0]]
# quadratic
c[2].STATUS=1
m.solve(disp=False)
p2 = [c[2].value[0],c[1].value[0],c[0].value[0]]
# cubic
c[3].STATUS=1
m.solve(disp=False)
p3 = [c[3].value[0],c[2].value[0],c[1].value[0],c[0].value[0]]
# plot fit
plt.plot(xm,ym,'ko',markersize=10)
xp = np.linspace(0,5,100)
plt.plot(xp,np.polyval(p1,xp),'b--',linewidth=2)
plt.plot(xp,np.polyval(p2,xp),'r--',linewidth=3)
plt.plot(xp,np.polyval(p3,xp),'g:',linewidth=2)
plt.legend(['Data','Linear','Quadratic','Cubic'],loc='best')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# measurements
xm = np.array([0,1,2,3,4,5])
ym = np.array([0.1,0.2,0.3,0.5,0.8,2.0])
# GEKKO model
m = GEKKO()
# parameters
x = m.Param(value=xm)
a = m.FV()
a.STATUS=1
# variables
y = m.CV(value=ym)
y.FSTATUS=1
# regression equation
m.Equation(y==0.1*m.exp(a*x))
# regression mode
m.options.IMODE = 2
# optimize
m.solve(disp=False)
# print parameters
print('Optimized, a = ' + str(a.value[0]))
plt.plot(xm,ym,'bo')
plt.plot(xm,y.value,'r-')
plt.show()
Gekko Brain Module Simplifies Code
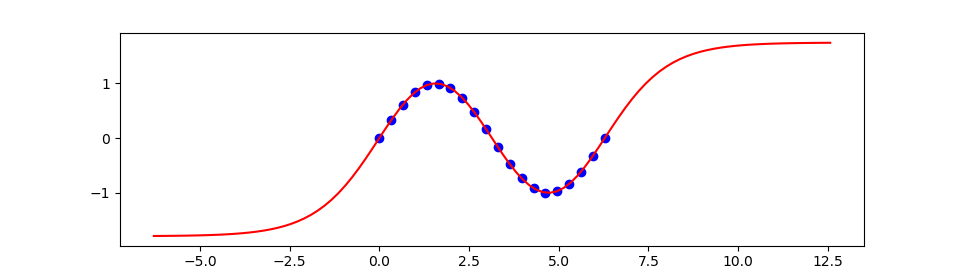
import numpy as np
import matplotlib.pyplot as plt
# generate training data
x = np.linspace(0.0,2*np.pi,20)
y = np.sin(x)
x = np.array(x)
y = np.array(y)
b = brain.Brain()
b.input_layer(1)
b.layer(linear=2)
b.layer(tanh=3)
b.layer(linear=2)
b.output_layer(1)
b.learn(x,y) # train
xp = np.linspace(-2*np.pi,4*np.pi,100)
yp = b.think(xp) # validate
plt.figure()
plt.plot(x,y,'bo')
plt.plot(xp,yp[0],'r-')
plt.show()
Hybrid Machine Learning: Cosine Activation
import numpy as np
import matplotlib.pyplot as plt
# generate training data
x = np.linspace(0.0,2*np.pi,20)
y = np.sin(x)
# option for fitting function
select = False # True / False
if select:
# Size with cosine function
nin = 1 # inputs
n1 = 1 # hidden layer 1 (linear)
n2 = 1 # hidden layer 2 (nonlinear)
n3 = 1 # hidden layer 3 (linear)
nout = 1 # outputs
else:
# Size with hyperbolic tangent function
nin = 1 # inputs
n1 = 2 # hidden layer 1 (linear)
n2 = 2 # hidden layer 2 (nonlinear)
n3 = 2 # hidden layer 3 (linear)
nout = 1 # outputs
# Initialize gekko
train = GEKKO()
test = GEKKO()
model = [train,test]
for m in model:
# input(s)
m.inpt = m.Param()
# layer 1
m.w1 = m.Array(m.FV, (nin,n1))
m.l1 = [m.Intermediate(m.w1[0,i]*m.inpt) for i in range(n1)]
# layer 2
m.w2a = m.Array(m.FV, (n1,n2))
m.w2b = m.Array(m.FV, (n1,n2))
if select:
m.l2 = [m.Intermediate(sum([m.cos(m.w2a[j,i]+m.w2b[j,i]*m.l1[j]) \
for j in range(n1)])) for i in range(n2)]
else:
m.l2 = [m.Intermediate(sum([m.tanh(m.w2a[j,i]+m.w2b[j,i]*m.l1[j]) \
for j in range(n1)])) for i in range(n2)]
# layer 3
m.w3 = m.Array(m.FV, (n2,n3))
m.l3 = [m.Intermediate(sum([m.w3[j,i]*m.l2[j] \
for j in range(n2)])) for i in range(n3)]
# output(s)
m.outpt = m.CV()
m.Equation(m.outpt==sum([m.l3[i] for i in range(n3)]))
# flatten matrices
m.w1 = m.w1.flatten()
m.w2a = m.w2a.flatten()
m.w2b = m.w2b.flatten()
m.w3 = m.w3.flatten()
# Fit parameter weights
m = train
m.inpt.value=x
m.outpt.value=y
m.outpt.FSTATUS = 1
for i in range(len(m.w1)):
m.w1[i].FSTATUS=1
m.w1[i].STATUS=1
m.w1[i].MEAS=1.0
for i in range(len(m.w2a)):
m.w2a[i].STATUS=1
m.w2b[i].STATUS=1
m.w2a[i].FSTATUS=1
m.w2b[i].FSTATUS=1
m.w2a[i].MEAS=1.0
m.w2b[i].MEAS=0.5
for i in range(len(m.w3)):
m.w3[i].FSTATUS=1
m.w3[i].STATUS=1
m.w3[i].MEAS=1.0
m.options.IMODE = 2
m.options.SOLVER = 3
m.options.EV_TYPE = 2
m.solve(disp=False)
# Test sample points
m = test
for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
print('w1['+str(i)+']: '+str(m.w1[i].MEAS))
for i in range(len(m.w2a)):
m.w2a[i].MEAS=train.w2a[i].NEWVAL
m.w2b[i].MEAS=train.w2b[i].NEWVAL
m.w2a[i].FSTATUS = 1
m.w2b[i].FSTATUS = 1
print('w2a['+str(i)+']: '+str(m.w2a[i].MEAS))
print('w2b['+str(i)+']: '+str(m.w2b[i].MEAS))
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
print('w3['+str(i)+']: '+str(m.w3[i].MEAS))
m.inpt.value=np.linspace(-2*np.pi,4*np.pi,100)
m.options.IMODE = 2
m.options.SOLVER = 3
m.solve(disp=False)
plt.figure()
plt.plot(x,y,'bo')
plt.plot(test.inpt.value,test.outpt.value,'r-')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO()
k = 10
m.time = np.linspace(0,20,100)
y = m.Var(value=5)
t = m.Param(value=m.time)
m.Equation(k*y.dt()==-t*y)
m.options.IMODE=4
m.solve(disp=False)
plt.plot(m.time,y.value)
plt.xlabel('time')
plt.ylabel('y')
plt.show()
$$ \min x_1 x_4 (x_1 + x_2 + x_3) + x_3 $$
$$ \mathrm{subject\;to} \quad x_1 x_2 x_3 x_4 \ge 25$$
$$\quad x_1^2 + x_2^2 + x_3^2 + x_4^2 = 40$$
$$\quad 1 \le x_1, x_2, x_3, x_4 \le 5$$
$$\quad x_0 = (1,5,5,1)$$
Solve this optimization problem from a web-browser interface or with GEKKO Python.
import numpy as np
#Initialize Model
m = GEKKO()
#help(m)
#define parameter
eq = m.Param(value=40)
#initialize variables
x1,x2,x3,x4 = [m.Var() for i in range(4)]
#initial values
x1.value = 1
x2.value = 5
x3.value = 5
x4.value = 1
# lower bounds
x1.lower = 1
x2.lower = 1
x3.lower = 1
x4.lower = 1
# upper bounds
x1.upper = 5
x2.upper = 5
x3.upper = 5
x4.upper = 5
#Equations
m.Equation(x1*x2*x3*x4>=25)
m.Equation(x1**2+x2**2+x3**2+x4**2==eq)
#Objective
m.Obj(x1*x4*(x1+x2+x3)+x3)
#Set global options
m.options.IMODE = 3 #steady state optimization
#Solve simulation
m.solve()
#Results
print('')
print('Results')
print('x1: ' + str(x1.value))
print('x2: ' + str(x2.value))
print('x3: ' + str(x3.value))
print('x4: ' + str(x4.value))
m = GEKKO() # Initialize gekko
m.options.SOLVER=1 # APOPT is an MINLP solver
# optional solver settings with APOPT
m.solver_options = ['minlp_maximum_iterations 500', \
# minlp iterations with integer solution
'minlp_max_iter_with_int_sol 10', \
# treat minlp as nlp
'minlp_as_nlp 0', \
# nlp sub-problem max iterations
'nlp_maximum_iterations 50', \
# 1 = depth first, 2 = breadth first
'minlp_branch_method 1', \
# maximum deviation from whole number
'minlp_integer_tol 0.05', \
# covergence tolerance
'minlp_gap_tol 0.01']
# Initialize variables
x1 = m.Var(value=1,lb=1,ub=5)
x2 = m.Var(value=5,lb=1,ub=5)
# Integer constraints for x3 and x4
x3 = m.Var(value=5,lb=1,ub=5,integer=True)
x4 = m.Var(value=1,lb=1,ub=5,integer=True)
# Equations
m.Equation(x1*x2*x3*x4>=25)
m.Equation(x1**2+x2**2+x3**2+x4**2==40)
m.Obj(x1*x4*(x1+x2+x3)+x3) # Objective
m.solve(disp=False) # Solve
print('Results')
print('x1: ' + str(x1.value))
print('x2: ' + str(x2.value))
print('x3: ' + str(x3.value))
print('x4: ' + str(x4.value))
print('Objective: ' + str(m.options.objfcnval))
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO() # initialize gekko
nt = 101
m.time = np.linspace(0,2,nt)
# Variables
x1 = m.Var(value=1)
x2 = m.Var(value=0)
u = m.Var(value=0,lb=-1,ub=1)
p = np.zeros(nt) # mark final time point
p[-1] = 1.0
final = m.Param(value=p)
# Equations
m.Equation(x1.dt()==u)
m.Equation(x2.dt()==0.5*x1**2)
m.Obj(x2*final) # Objective function
m.options.IMODE = 6 # optimal control mode
m.solve(disp=False) # solve
plt.figure(1) # plot results
plt.plot(m.time,x1.value,'k-',label=r'$x_1$')
plt.plot(m.time,x2.value,'b-',label=r'$x_2$')
plt.plot(m.time,u.value,'r--',label=r'$u$')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# create GEKKO model
m = GEKKO()
# time points
n=501
m.time = np.linspace(0,10,n)
# constants
E,c,r,k,U_max = 1,17.5,0.71,80.5,20
# fishing rate
u = m.MV(value=1,lb=0,ub=1)
u.STATUS = 1
u.DCOST = 0
x = m.Var(value=70) # fish population
# fish population balance
m.Equation(x.dt() == r*x*(1-x/k)-u*U_max)
J = m.Var(value=0) # objective (profit)
Jf = m.FV() # final objective
Jf.STATUS = 1
m.Connection(Jf,J,pos2='end')
m.Equation(J.dt() == (E-c/x)*u*U_max)
m.Obj(-Jf) # maximize profit
m.options.IMODE = 6 # optimal control
m.options.NODES = 3 # collocation nodes
m.options.SOLVER = 3 # solver (IPOPT)
m.solve(disp=False) # Solve
print('Optimal Profit: ' + str(Jf.value[0]))
plt.figure(1) # plot results
plt.subplot(2,1,1)
plt.plot(m.time,J.value,'r--',label='profit')
plt.plot(m.time,x.value,'b-',label='fish')
plt.legend()
plt.subplot(2,1,2)
plt.plot(m.time,u.value,'k--',label='rate')
plt.xlabel('Time (yr)')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO() # initialize GEKKO
nt = 501
m.time = np.linspace(0,1,nt)
# Variables
x1 = m.Var(value=np.pi/2.0)
x2 = m.Var(value=4.0)
x3 = m.Var(value=0.0)
p = np.zeros(nt) # final time = 1
p[-1] = 1.0
final = m.Param(value=p)
# optimize final time
tf = m.FV(value=1.0,lb=0.1,ub=100.0)
tf.STATUS = 1
# control changes every time period
u = m.MV(value=0,lb=-2,ub=2)
u.STATUS = 1
m.Equation(x1.dt()==u*tf)
m.Equation(x2.dt()==m.cos(x1)*tf)
m.Equation(x3.dt()==m.sin(x1)*tf)
m.Equation(x2*final<=0)
m.Equation(x3*final<=0)
m.Obj(tf)
m.options.IMODE = 6
m.solve(disp=False)
print('Final Time: ' + str(tf.value[0]))
tm = np.linspace(0,tf.value[0],nt)
plt.figure(1)
plt.plot(tm,x1.value,'k-',label=r'$x_1$')
plt.plot(tm,x2.value,'b-',label=r'$x_2$')
plt.plot(tm,x3.value,'g--',label=r'$x_3$')
plt.plot(tm,u.value,'r--',label=r'$u$')
plt.legend(loc='best')
plt.xlabel('Time')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO()
tf = 40
m.time = np.linspace(0,tf,2*tf+1)
step = np.zeros(2*tf+1)
step[3:40] = 2.0
step[40:] = 5.0
# Controller model
Kc = 15.0 # controller gain
tauI = 2.0 # controller reset time
tauD = 1.0 # derivative constant
OP_0 = m.Const(value=0.0) # OP bias
OP = m.Var(value=0.0) # controller output
PV = m.Var(value=0.0) # process variable
SP = m.Param(value=step) # set point
Intgl = m.Var(value=0.0) # integral of the error
err = m.Intermediate(SP-PV) # set point error
m.Equation(Intgl.dt()==err) # integral of the error
m.Equation(OP == OP_0 + Kc*err + (Kc/tauI)*Intgl - PV.dt())
# Process model
Kp = 0.5 # process gain
tauP = 10.0 # process time constant
m.Equation(tauP*PV.dt() + PV == Kp*OP)
m.options.IMODE=4
m.solve(disp=False)
plt.figure()
plt.subplot(2,1,1)
plt.plot(m.time,OP.value,'b:',label='OP')
plt.ylabel('Output')
plt.legend()
plt.subplot(2,1,2)
plt.plot(m.time,SP.value,'k-',label='SP')
plt.plot(m.time,PV.value,'r--',label='PV')
plt.xlabel('Time (sec)')
plt.ylabel('Process')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Generate "data" with process simulation
nt = 51
# input steps
u_meas = np.zeros(nt)
u_meas[3:10] = 1.0
u_meas[10:20] = 2.0
u_meas[20:40] = 0.5
u_meas[40:] = 3.0
# simulation model
p = GEKKO()
p.time = np.linspace(0,10,nt)
n = 1 #process model order
# Parameters
steps = np.zeros(n)
p.u = p.MV(value=u_meas)
p.u.FSTATUS=1
p.K = p.Param(value=1) #gain
p.tau = p.Param(value=5) #time constant
# Intermediate
p.x = [p.Intermediate(p.u)]
# Variables
p.x.extend([p.Var() for _ in range(n)]) #state variables
p.y = p.SV() #measurement
# Equations
p.Equations([p.tau/n * p.x[i+1].dt() == -p.x[i+1] + p.x[i] for i in range(n)])
p.Equation(p.y == p.K * p.x[n])
# Simulate
p.options.IMODE = 4
p.solve(disp=False)
# add measurement noise
y_meas = (np.random.rand(nt)-0.5)*0.2
for i in range(nt):
y_meas[i] += p.y.value[i]
plt.plot(p.time,u_meas,'b:',label='Input (u) meas')
plt.plot(p.time,y_meas,'ro',label='Output (y) meas')
plt.plot(p.time,p.y.value,'k-',label='Output (y) actual')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Estimator Model
m = GEKKO()
nt=51 # number of time steps
m.time = np.linspace(0,10,nt)
# input steps
u_meas = np.zeros(nt)
# simulated measurements
y_meas = (np.random.rand(nt)-0.5)*0.2
# Parameters
m.u = m.MV(value=u_meas) #input
m.K = m.FV(value=1, lb=1, ub=3) # gain
m.tau = m.FV(value=5, lb=1, ub=10) # time constant
# Variables
m.x = m.SV() #state variable
m.y = m.CV(value=y_meas) #measurement
# Equations
m.Equations([m.tau * m.x.dt() == -m.x + m.u,
m.y == m.K * m.x])
# Options
m.options.IMODE = 5 #MHE
m.options.EV_TYPE = 1
# STATUS = 0, optimizer doesn't adjust value
# STATUS = 1, optimizer can adjust
m.u.STATUS = 0
m.K.STATUS = 1
m.tau.STATUS = 1
m.y.STATUS = 1
# FSTATUS = 0, no measurement
# FSTATUS = 1, measurement used to update model
m.u.FSTATUS = 1
m.K.FSTATUS = 0
m.tau.FSTATUS = 0
m.y.FSTATUS = 1
# DMAX = maximum movement each cycle
m.K.DMAX = 2.0
m.tau.DMAX = 4.0
# MEAS_GAP = dead-band for measurement / model mismatch
m.y.MEAS_GAP = 0.25
# solve
m.solve(disp=True)
# Plot results
plt.subplot(2,1,1)
plt.plot(m.time,u_meas,'b:',label='Input (u) meas')
plt.legend()
plt.subplot(2,1,2)
plt.plot(m.time,y_meas,'gx',label='Output (y) meas')
plt.plot(m.time,m.y.value,'r--',label='Output (y) estimated')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO()
m.time = np.linspace(0,20,41)
# Parameters
mass = 500
b = m.Param(value=50)
K = m.Param(value=0.8)
# Manipulated variable
p = m.MV(value=0, lb=0, ub=100)
p.STATUS = 1 # allow optimizer to change
p.DCOST = 0.1 # smooth out gas pedal movement
p.DMAX = 20 # slow down change of gas pedal
# Controlled Variable
v = m.CV(value=0)
v.STATUS = 1 # add the SP to the objective
m.options.CV_TYPE = 2 # squared error
v.SP = 40 # set point
v.TR_INIT = 1 # set point trajectory
v.TAU = 5 # time constant of trajectory
# Process model
m.Equation(mass*v.dt() == -v*b + K*b*p)
m.options.IMODE = 6 # control
m.solve(disp=False)
# get additional solution information
import json
with open(m.path+'//results.json') as f:
results = json.load(f)
plt.figure()
plt.subplot(2,1,1)
plt.plot(m.time,p.value,'b-',label='MV Optimized')
plt.legend()
plt.ylabel('Input')
plt.subplot(2,1,2)
plt.plot(m.time,results['v1.tr'],'k-',label='Reference Trajectory')
plt.plot(m.time,v.value,'r--',label='CV Response')
plt.ylabel('Output')
plt.xlabel('Time')
plt.legend(loc='best')
plt.show()
m = GEKKO() # create GEKKO model
print('--------- Follow local path to view files --------------')
print(m.path) # show source file path
m.open_folder()
print('--------------------------------------------------------')
# test application
u = m.FV(value=5,name='u') # define fixed value
x = m.SV(name='state') # define state variable
m.Equation(x==u) # define equation
m.options.COLDSTART = 1 # coldstart option
m.options.DIAGLEVEL = 0 # diagnostic level (0-10)
m.options.MAX_ITER = 500 # adjust maximum iterations
m.options.SENSITIVITY = 1 # sensitivity analysis
m.options.SOLVER = 1 # change solver (1=APOPT,3=IPOPT)
m.solve(disp=True)
print('x: ' + str(x.value)) # print variable value
Learn GEKKO Python with Online Course
The Dynamic Optimization Course is graduate level course taught in three modules to introduce concepts in:
- mathematical modeling (3 weeks)
- machine learning, estimation (3 weeks)
- control, optimization (3 weeks)
There are many other applications and instructional material posted to this freely available course web-site. The online course is generally offered starting each year in January. There are two course projects that include the advanced temperature control lab (1st project) and a project that is a group choice (2nd project). Below is an example student presentation at the end of the course. It is representative of the modeling, estimation, and control methods that are taught in the dynamic optimization course.



