APMonitor

! Continuously Stirred Tank Reactor with energy
!   balance and Van de Vusse reactions A->B->C and 2A->D
!
! Optimization of Van de Vusse Reaction Kinetics Using Semibatch Reactor Operation
! G. A. Ridlehoover , R. C. Seagrave
! Ind. Eng. Chem. Fundamen., 1973, 12 (4), pp 444–447
! DOI: 10.1021/i160048a008
! Publication Date: November 1973
!
Model
  Parameters
    F = 14.19         ! Feed rate (l/hr)
    Qk = -1579.5      ! Jacket cooling rate (kJ/hr)
    Ca0 =  5.1        ! Inlet feed concentration (mol/m^3)
    T0 = 104.9        ! Inlet feed temperature (degC)

    k10 = 1.287e10    ! A->B Pre-exponential factor (1/hr)
    k20 = 1.287e10    ! B->C Pre-exponential factor (1/hr)
    k30 = 9.043e9     ! 2A->D Pre-exponential factor (1/hr)
    E1 = 9758.3       ! A->B Activation Energy (K)
    E2 = 9758.3       ! B->C Activation Energy (K)
    E3 = 8560         ! 2A->D Activation Energy (K)
    dHr1 = 4.2        ! A->B Heat of Reaction (kJ/mol A)
    dHr2 = -11        ! B->C Heat of Reaction (kJ/mol B)
    dHr3 = -41.85     ! 2A->D Heat of Reaction (kJ/mol A)
    rho = 0.9342      ! density (kg/l)
    Cp = 3.01         ! Heat capacity of reactants (kJ/kg-K)
    kw = 4032         ! Heat transfer coefficient (kJ/h-K-m^2)
    AR = .215         ! Area of jacket cooling (m^2)
    VR = 10.0         ! Reactor volume (l)
    mK = 5            ! Mass of cooling (kg)
    CpK = 2           ! Heat capacity of cooling (kJ/kg-K)
  End Parameters

  Variables
    ! Differential States
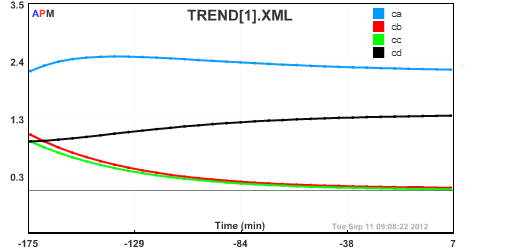
    Ca = 2.2291       ! Concentration of A in CSTR (mol/l)
    Cb = 1.0417       ! Concentration of B in CSTR (mol/l)
    Cc = 0.91397      ! Concentration of C in CSTR (mol/l)
    Cd = 0.91520      ! Concentration of D in CSTR (mol/l)

    T  = 79.591  ! Temperature in CSTR (degC)
    Tk = 77.69   ! Cooling jacket temperature (degC)
  End Variables

  Intermediates
    k1 = k10*exp(-E1/(T+273.15))
    k2 = k20*exp(-E2/(T+273.15))
    k3 = k30*exp(-E3/(T+273.15))

    r1 = k1*VR*Ca
    r2 = k2*VR*Cb
    r3 = k3*VR*Ca^2
  End Intermediates

  Equations
    ! note: the $ denotes time differential
    !  (e.g. $x is dx/dt)

    ! species balances
    VR * $Ca = -r1 - 2*r3 + F*(Ca0-Ca)
    VR * $Cb =  r1   - r2 - F*Cb
    VR * $Cc =  r2        - F*Cc
    VR * $Cd =  r3        - F*Cd

    ! energy balance on reactor
    rho*Cp*VR*$T = F*rho*Cp*(T0 - T) &
                   - r1*dHr1         &
                   - r2*dHr2         &
                   - r3*dHr3         &
                   + kw*AR*(Tk - T)

    ! energy balance on cooling
    mK * CpK * $Tk = Qk + kw*AR*(T - Tk)
  End Equations
End Model

File *.info
 F, T0
 F, F
 F, Ca0
 F, T0
 F, Qk
 S, Tk
 S, Ca
 S, Cb
 S, Cc
 S, Cd
 C, T
End File

File overrides.dbs
 nlc.web = 2
 nlc.ctrl_units = 3
 nlc.hist_units = 2
 nlc.cv_type = 1
 nlc.ev_type = 1
 nlc.reqctrlmode = 1
 nlc.csv_read = 1
 nlc.hist_hor = 100
 nlc.web_plot_freq = 10
 nlc.nodes = 2
 nlc.imode = 7
End File

File *.csv
time
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3
End File